Преодоление ограничения линейной разделимости
К концу 1960-х годов проблема линейной разделимости была хорошо понята. К тому же, было известно, что это серьезное ограничение представляемости однослойными сетями можно преодолеть, добавив дополнительные слои. Например, двухслойные сети можно получить каскадным соединением двух однослойных сетей. Они способны выполнять более общие классификации, отделяя те точки, которые содержатся в выпуклых ограниченных или неограниченных областях. Область называется выпуклой, если для любых двух ее точек соединяющий их отрезок целиком лежит в области. Область называется ограниченной, если ее можно заключить в некоторый круг. Неограниченную область невозможно заключить внутрь круга (например, область между двумя параллельными линиями). Примеры выпуклых ограниченных и неограниченных областей представлены на рис. 2.6.
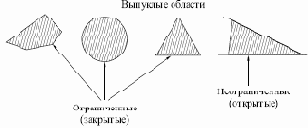
Рис. 2.6.
Чтобы уточнить требование выпуклости, рассмотрим простую двуслойную сеть с двумя входами, которые подведены к двум нейронам первого слоя, соединенными с единственным нейроном в слое 2 (см. рис. 2.7а). Пусть порог выходного нейрона равен 0,75, а оба его веса равны 0,5. В этом случае для того, чтобы порог был превышен и на выходе появилась единица, требуется, чтобы оба нейрона первого уровня на выходе имели единицу. Таким образом, выходной нейрон реализует логическую функцию И. На рис. 2.7а каждый нейрон слоя 1 разбивает плоскость


Точки, не составляющие выпуклой области, не могут быть отделены от других точек плоскости двухслойной сетью.
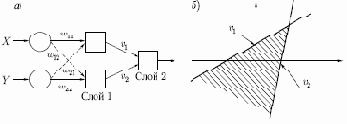
Рис. 2.7.
Нейрон второго слоя не ограничен функцией И. Он может реализовывать многие другие функции при подходящем выборе весов и порога. Например, можно сделать так, чтобы единичный выход любого из нейронов первого слоя приводил к появлению единицы на выходе нейрона второго слоя, реализовав тем самым логическое ИЛИ. Например, имеется 16 двоичных функций от двух переменных. Если выбирать подходящим образом веса и порог, то можно воспроизвести 14 из них (все, кроме ИСКЛЮЧАЮЩЕЕ ИЛИ и ИСКЛЮЧАЮЩЕЕ НЕТ).
Входы не обязательно должны быть двоичными. Вектор непрерывных входов может представлять собой произвольную точку на плоскости






Трехслойная сеть, впрочем, есть более общий случай. Ее классифицирующие возможности ограничены лишь числом искусственных нейронов и весов. Ограничения на выпуклость отсутствуют. Теперь нейрон третьего слоя принимает в качестве входа набор выпуклых многоугольников, и их логическая комбинация может быть невыпуклой. На рис. 2.8б
иллюстрируется ситуация, когда два треугольника A и B, скомбинированные с помощью функций "A и не B", задают невыпуклую область. При добавлении нейронов и весов число сторон многоугольников может неограниченно возрастать. Это позволяет аппроксимировать область любой формы с любой точностью. Вдобавок, не все выходные области второго слоя должны пересекаться. Возможно, следовательно, объединять различные области, выпуклые и невыпуклые, выдавая на выходе единицу всякий раз, когда входной вектор принадлежит одной из них.
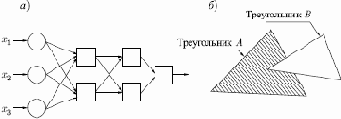
Рис. 2.8.
Несмотря на то, что возможности многослойных сетей были известны давно, в течение многих лет не было теоретически обоснованного алгоритма для настройки их весов. В последующих главах мы детально изучим многослойные обучающие алгоритмы, но сейчас достаточно понимать суть проблемы и знать, что исследования привели к определенным результатам.