Предварительная обработка входных векторов

Весьма желательно (хотя и не обязательно) нормализовать входные векторы перед тем, как предъявлять их сети. Операция выполняется с помощью деления каждой компоненты входного вектора на длину вектора. Эта длина находится извлечением квадратного корня из суммы квадратов компонент вектора. В алгебраической записи

(1)

Таким образом, входной вектор превращается в единичный вектор с тем же самым направлением, т.е. в вектор единичной длины в

-мерном пространстве.

Уравнение (1) обобщает хорошо известный случай двух измерений, когда длина вектора равна гипотенузе прямоугольного треугольника, образованного его

и компонентами, как это следует из известной теоремы Пифагора. На рис. 6.2 такой двумерный вектор

представлен в координатах

, причем координата

равна четырем, а координата

— трем. Квадратный корень из суммы квадратов этих компонент равен пяти. Деление каждой компоненты на пять дает вектор с компонентами 4/5 и 3/5, где

указывает в том же направлении, что и

, но имеет единичную длину.

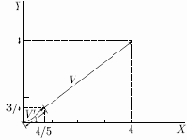
Рис. 6.2. 

На рис. 6.3 показано несколько единичных векторов. Они оканчиваются в точках единичной окружности (окружности единичного радиуса), а это происходит, когда у сети лишь два входа. В случае трех входов векторы представлялись бы стрелками, оканчивающимися на поверхности единичной сферы. Такие представления могут быть перенесены на сети, имеющие произвольное число входов, где каждый входной вектор является стрелкой, оканчивающейся на поверхности единичной гиперсферы (полезной абстракцией, хотя и не допускающей непосредственной визуализации).

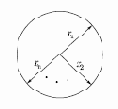
Рис. 6.3. 

При обучении слоя Кохонена на вход подается входной вектор и вычисляются его скалярные произведения с векторами весов, связанными со всеми нейронами Кохонена. Нейрон с максимальным значением скалярного произведения объявляется "победителем", и его веса подстраиваются. Так как скалярное произведение, используемое для вычисления величин

, является мерой сходства между входным вектором и вектором весов, то процесс обучения состоит в выборе нейрона Кохонена с весовым вектором, наиболее близким к входному вектору, и дальнейшем приближении весового вектора к входному.

Снова отметим, что процесс является самообучением, выполняемым без учителя. Сеть самоорганизуется таким образом, что данный нейрон Кохонена имеет максимальный выход для данного входного вектора. Уравнение, описывающее процесс обучения, имеет следующий вид:



где — новое значение веса, соединяющего входную компоненту с выигравшим нейроном; — предыдущее значение этого веса; — коэффициент скорости обучения, который может варьироваться в процессе обучения.

Каждый вес, связанный с выигравшим нейроном Кохонена, изменяется пропорционально разности между его величиной и величиной входа, к которому он присоединен. Направление изменения минимизирует разность между весом и его входом.

На рис. 6.4 этот процесс показан геометрически в двумерном виде. Сначала ищем вектор , для этого проводится отрезок из конца в конец . Затем этот вектор укорачиваем умножением его на скалярную величину , меньшую единицы, в результате чего получаем вектор изменения . Окончательно новый весовой вектор

является отрезком, направленным из начала координат в конец вектора . Отсюда можно видеть, что эффект обучения состоит во вращении весового вектора в направлении входного вектора без существенного изменения его длины.


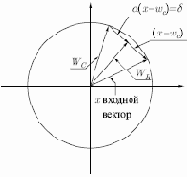
Рис. 6.4. 

Переменная является коэффициентом скорости обучения, который вначале обычно равен и может постепенно уменьшаться в процессе обучения. Это позволяет делать большие начальные шаги для быстрого грубого обучения и меньшие шаги при подходе к окончательной величине.

Если бы с каждым нейроном Кохонена ассоциировался один входной вектор, то слой Кохонена мог бы быть обучен с помощью одного вычисления на вес. Веса нейрона-победителя приравнивались бы к компонентам обучающего вектора (). Как правило, обучающее множество включает много сходных между собой входных векторов, и сеть должна быть обучена активировать один и тот же нейрон Кохонена для каждого из них. В этом случае веса этого нейрона должны вычисляться усреднением входных векторов, которые его активируют. Постепенное уменьшение величины уменьшает воздействие каждого обучающего шага, и окончательное значение будет средней величиной от входных векторов, на которых происходит обучение.Таким образом, веса, ассоциированные с нейроном, примут значение вблизи "центра" входных векторов, для которых данный нейрон является "победителем".


Содержание раздела

---

---

---

Главная сайта

---